机器学习-可扩展流形学习方法SUDE

·

一、前置知识

1、 K 近邻集合（KNN）

定义：给定一个点 xix_ixi 与正整数 KKK，它的 K 近邻集合
$$
\mathcal{N}K(i) = \operatorname*{arg,Kmin}{j \neq i} ; d_{ij}
$$
即与 xix_ixi 距离最小的 KKK 个样本的索引集合（实现里通常包含自邻居）

2、反近邻计数（RNN）

定义：一个点 x_u 的 RNN 计数是
$$
\mathrm{RNN}(u)=\left|\left{,i\in{1,\dots,N};\big|; u\in \mathcal{N}_{k_1}(i)\right}\right|
$$
也就是“有多少别人的 KNN 集合把它包含进去”。RNN 能反映枢纽点（hub）：在高维/不均匀数据中，某些点会频繁出现在他人的近邻里，RNN 值大。

3、共享近邻（SNN）

核心思想：如果两个点 i,ji,ji,j 的邻居集合高度重合，那么它们“相似”的证据更强。

定义（加权版）：设
$$
N_i = \mathcal{N}{k_1}(i)、N_j = \mathcal{N}{k_1}(j)
$$
用 RNN 作为共享邻居的权重，则
$$
\mathrm{SNN}{ij} = \sum{u \in N_i \cap N_j} w(u),
\quad w(u) = \mathrm{RNN}(u)
$$
代码实现：对固定的 i，把每个候选 j 与 i 是否“共享近邻”转成 0/1 指示（np.isin(...).astype(int)），再把被共享的邻居位置用 rnn 加权并对行求和，得到行向量 snn[i,·]。

4、SNN 强度的归一化

为什么要归一化：不同 iii 的 SNN 数值尺度不同（取决于 Ni 的大小/密度/枢纽分布），直接拿来缩放距离不稳。

我们不妨做个测试来验证SNN归一化的必要性：

这是原本的散点图（测试数据集）

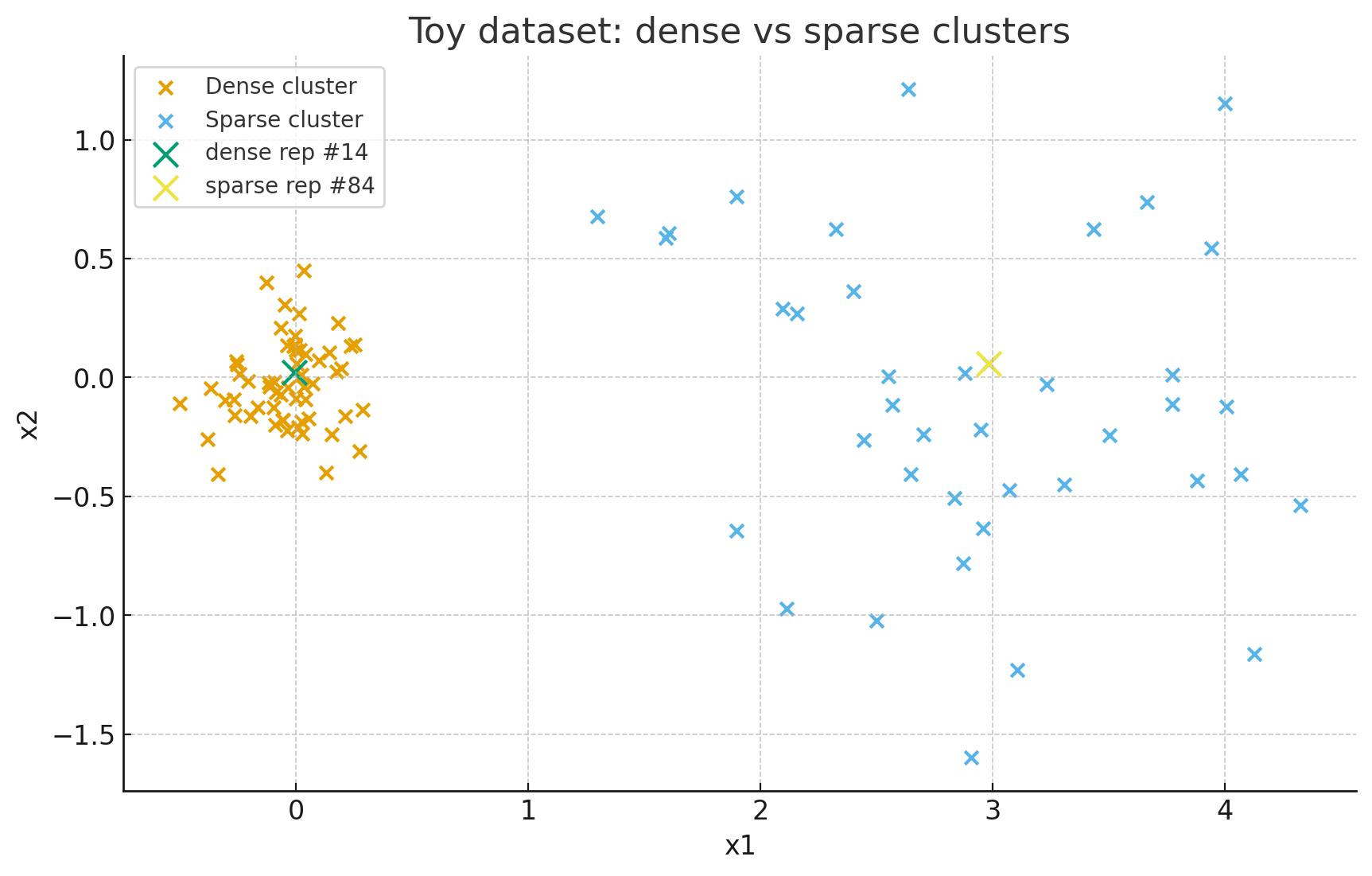
这是未经过归一化处理后的SNN

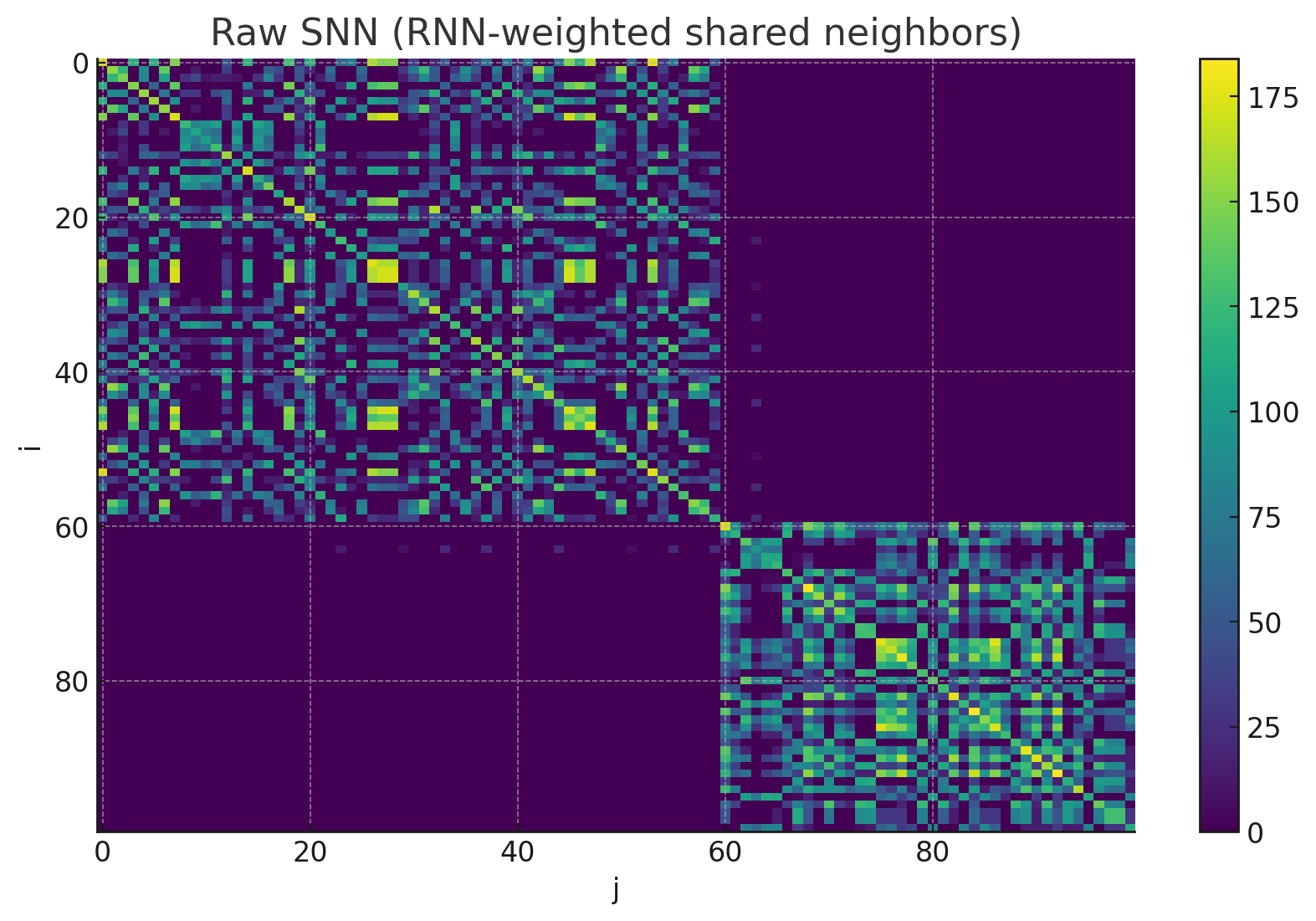
这是经过归一化处理的SNN

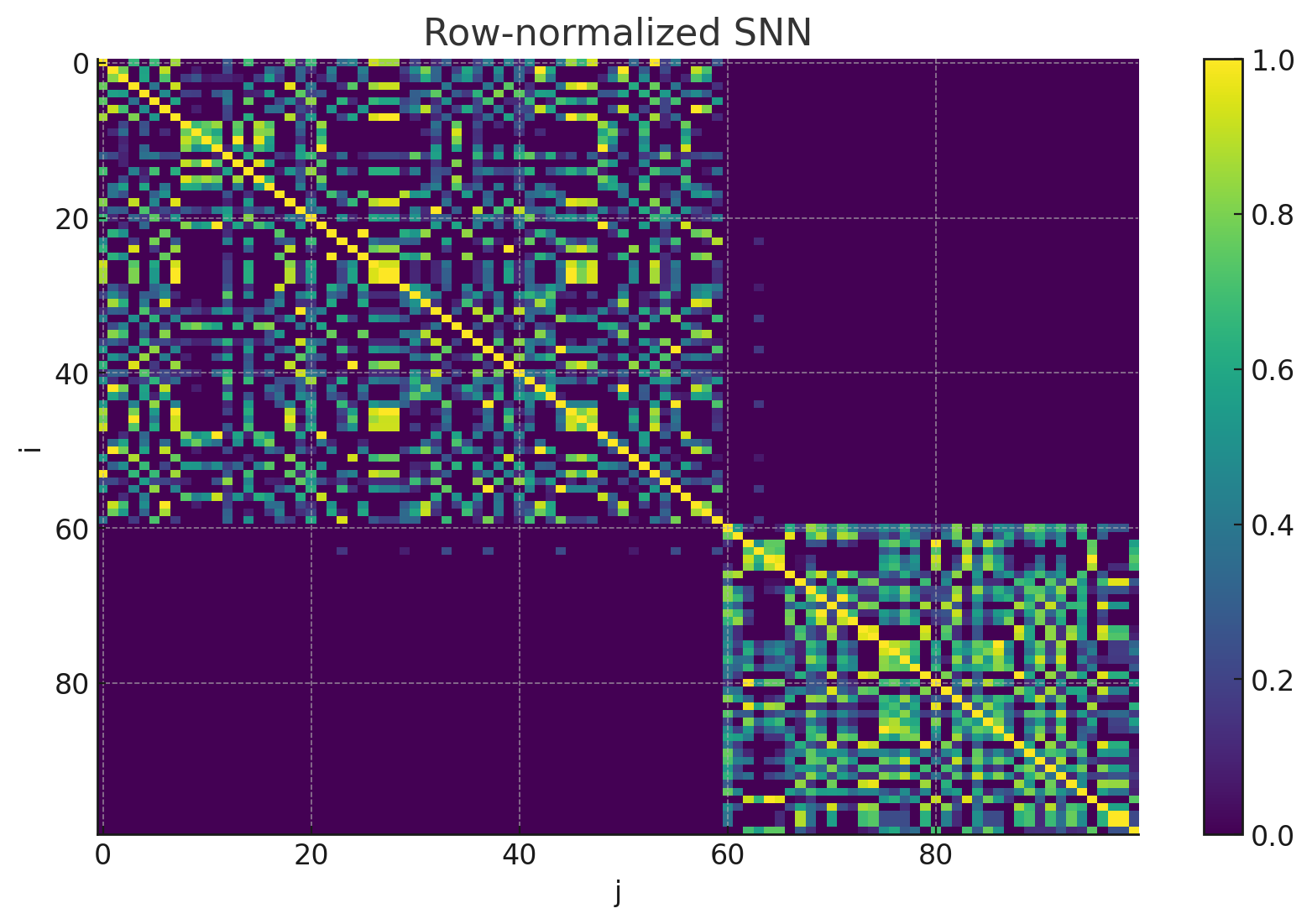
显而易见，归一化处理后不同 i 的数值被压到相同尺度 [0,1]，便于后续用来“软缩放”距离。

5、软缩放距离

目的：共享近邻越强（越像同类），就把它们的高维距离乘一个小因子缩短；共享弱的点对则缩放因子接近 1，几乎不变。

定义：给定原始欧氏距离 与归一化后的SNN
$$
d_{ij} 、\tilde{\mathrm{SNN}}{ij}
$$
定义
$$
\tilde{\mathrm{d}}{ij}​=(1−\tilde{\mathrm{SNN}}{ij}​)agg_coef⋅d_{ij}​,agg_coef>0.
$$
性质：

6、自适应带宽

目的：在密度不均匀的数据上，让每个点有自己的“局部尺度”，避免用全局 σ造成稠密区过拟合/稀疏区欠拟合。

定义：对每个 i，用它经软缩放后的最近 k2个距离的均值当作局部尺度，再平方得到方差：
$$
\sigma_i^2 ;=; \left( \frac{1}{k_2} \sum_{j \in \mathcal{N}{k_2}^{(\mathrm{mod})}(i)} \tilde{d}{ij} \right)^2
$$
在稠密区，σi 小，核变“窄”，只加强很近的点；在稀疏区，σi 大，核“宽”，避免把一切都判为极不相似。

7、高斯核相似度

公式：
$$
P_{ij} ;\propto; \exp!\left(-\tfrac{1}{2}\tfrac{\tilde{d}{ij}^2}{\sigma_i^2}\right),
\qquad j \in \mathcal{N}{k_2}^{(\mathrm{mod})}(i)
$$
其他位置为 0（保持稀疏）。

8、稀疏矩阵的 CSR 表示

概念：CSR 用三组向量存矩阵的非零项：

• row：每个非零的行索引（按行块存储）
• col：每个非零的列索引
• data：对应的非零值
  配合内部指针（indptr）就能重建稀疏矩阵，矩阵–向量乘法/按行切片都很快。

二、算法分析

1、PCA算法：

简介：

PCA 用于大规模或高维数据的降维初始化，目标是：

找方向（主成分）：在原始高维数据中，找到一组正交方向，使得数据在这些方向上的方差最大。

投影降维：把原始数据投影到前几个主成分方向上，得到低维表示，同时尽可能保留原始数据的结构信息。

流程：

零均值化：
对每个维度减去均值，让数据中心在原点。

计算协方差矩阵：（ 协方差是两个变量的线性相关性强度）
$$
C= \frac{1}{n} X^T X
$$
表示不同特征之间的相关性。

特征分解：
解出协方差矩阵的特征值和特征向量：

• 特征值 λ 表示该方向上的方差大小。
• 特征向量 M 表示该方向的坐标轴（主成分方向）。

排序选取：
将特征值按大小排序，取前 k 个最大特征值对应的特征向量，组成投影矩阵。

投影得到低维表示：
$$
Y=XMk
$$
其中
$$
M_k
$$
是前 k 个主成分向量。

2、PPS算法

简介：

选出一部分点（地标）参与嵌入学习，既能代表整体分布，又不会太密集。优先挑选 “重要点”（RNN 值高 = 在很多人的近邻里出现过 = 数据中心/高密度点）。每选一个地标，就把它周围的点（它的近邻）从候选列表里删掉，避免采样过于拥挤。最终得到的地标，既分散又代表数据核心结构。

流程：

1. 排序：按 rnn 从大到小排队，形成候选队列 id_sort。
2. 循环选点：
   • 取队首（当前 RNN 最大的点）作为一个地标，加入 id_samp。
   • 将这个点的近邻（根据 knn）加入一个待删除集合 rm_pts。
   • 如果 order > 1，继续扩展，把近邻的近邻也删掉。
   • 把这些点从候选队列 id_sort 中移除。
3. 重复：直到没有候选点。
4. 输出：得到一组分散、密度敏感的地标索引 id_samp。

3、地标上学习低维表示算法

低维：learning_s

流程：输入→建图→初始化→分块优化→输出

高维：learning_l

流程：

三、代码分析

1、PCA算法

import numpy as np


def init_pca(X, no_dims, contri):
    """
    对数据进行 PCA 预处理（用于大规模或高维数据的降维初始化）。

    参数：
    X        - N×D 的数据矩阵，每一行是一个样本，每一列是一个特征。
    no_dims  - 目标降维维度（至少保证结果维度 >= no_dims+1）。
    contri   - 累积方差贡献率阈值（例如 0.8 表示保留 80% 的方差信息）。
    """

    m = X.shape[1]                  # 原始特征维度数 D
    X = X - np.mean(X, axis=0)      # 1: 数据零均值化（减去每列的均值）

    # 2: 计算协方差矩阵 (D×D)，用于衡量各特征间的相关性
    C = np.cov(X, rowvar=False)     

    # 防止协方差矩阵中出现 NaN，替换为 0
    C[np.isnan(C)] = 0
    C[np.isinf(C)] = 0

    # 3: 对协方差矩阵做特征分解，得到特征值 lamda 和特征向量 M
    # 特征值表示该方向上的方差大小，特征向量表示主成分方向
    lamda, M = np.linalg.eig(C)
    lamda = np.real(lamda)          # 取实部（理论上应为实数，但数值计算可能有虚部）

    # 4: 确定最佳降维维度m
    if m < 2001:
        # 如果维度不超过 2000，使用所有特征值计算累计方差贡献率
        ind = np.where(np.cumsum(lamda) / sum(lamda) > contri)
    else:
        # 如果维度超过 2000，只取前 2000 个特征值估计贡献率（避免计算开销过大）
        ind = np.where(np.cumsum(lamda) / sum(lamda[:2000]) > contri)

    # bestDim 至少为 no_dims+1，同时也要满足贡献率阈值
    bestDim = max(no_dims + 1, int(ind[0][0]))

    # 5: 取前m个主成分方向（特征向量），并将数据投影到这些方向上
    mappedX = X @ np.real(M)[:, :bestDim]

    return mappedX  # 返回降维后的数据，形状 (N, m)

2、PPS算法

import numpy as np


def pps(knn, rnn, order):
    """
    Plum Pudding Sampling (PPS)
    返回选出的地标点索引集合。

    参数：
    knn    - N*k 的矩阵，每一行存储该点的 k 个最近邻索引。
    rnn    - 长度为 N 的数组，每个元素是该点作为别人近邻出现的次数（RNN值）。
    order  - 正整数，表示要剔除的邻居阶数。order=1 表示直接邻居，order=2 表示邻居的邻居也要剔除。
    """

    id_samp = []  
    # 存储最终选出的地标点索引

    id_sort = sorted(range(len(rnn)), key=lambda k: rnn[k], reverse=True)
    # 按 RNN 值从大到小对所有点排序，得到候选点队列
    # RNN 值高的点更“重要”，优先被选为地标

    while len(id_sort) > 0:  
        # 当还有候选点时，不断选择新地标
        id_samp.append(id_sort[0])  
        # 选出当前 RNN 最大的点作为一个地标

        rm_pts = [id_sort[0]]  
        # 待移除点集合，初始只包含刚选的地标

        for _ in range(order):  
            # 根据指定阶数，扩展要删除的邻域
            # knn[rm_pts]：取出 rm_pts 中点的近邻集合
            # flatten(把 多维数组 → 一维数组的拷贝) + tolist(numpy 数组 → Python 原生 list)：转为一维列表
            rm_pts.extend(knn[rm_pts].flatten().tolist())

        rm_pts = set(rm_pts)  
        # 转为集合，避免重复

        rm_id = np.where(np.isin(id_sort, list(rm_pts)))[0]
        # 找到候选队列 id_sort 中属于 rm_pts 的索引位置

        id_sort = [id_sort[i] for i in range(len(id_sort)) if i not in rm_id]
        # 从候选队列里剔除这些点，避免它们在后续被再次选为地标

    return id_samp  
    # 返回所有选中的地标点索引

learning_l

from sklearn.neighbors import NearestNeighbors
from scipy.sparse import diags           # 稀疏对角矩阵构造（用于度矩阵等）
from scipy.sparse import csr_matrix      # 压缩稀疏行矩阵（邻接/概率矩阵用这个省内存）
from scipy.spatial.distance import cdist # 成对距离（这里主要用欧氏距离）
from init_pca import init_pca            # 你自定义的 PCA 预降维（保留贡献率阈值）
from pca import pca                      # 线性 PCA 初始化
from mds import mds                      # 经典 MDS 初始化
import scipy.sparse.linalg as sp_linalg  # 稀疏矩阵特征分解
import numpy as np
import math


def learning_l(X_samp, k1, get_knn, rnn, id_samp, no_dims, initialize, agg_coef, T_epoch):
    """
    作用（地标的 block 版学习）：
      - 在地标子集 X_samp 上学习其低维嵌入 Y（维度 = no_dims）
      - 自适应确定地标层的近邻数 k2（用于构造高维概率 P）
      - 与 learning_s 的区别：这里对 P、Q 的梯度按“数据块”计算（降低峰值内存，适合更大 N）

    参数：
      X_samp     : (N, dim) 地标样本矩阵（从全体 X 中采样而来）
      k1         : 采样阶段的 K（>0 表示此时 get_knn / rnn / id_samp 可用；=0 表示无采样信息）
      get_knn    : (n, k1+1) 全数据的 KNN 索引矩阵（含自邻居），仅当 k1>0 时使用
      rnn        : (n,)      全数据的 RNN 计数（点作为别人近邻被命中的次数），仅当 k1>0 时使用
      id_samp    : (N,)      地标在原数据中的索引（映射 get_knn / rnn 用），仅当 k1>0 时使用
      no_dims    : 目标嵌入维度（Y 的列数）
      initialize : 初始嵌入方式：'le'（Laplacian Eigenmaps）、'pca'、'mds'
      agg_coef   : SNN 聚合系数，控制 (1 - SNN)^agg_coef 对高维距离的“软缩放”强度
      T_epoch    : 训练轮数

    返回：
      Y  : (N, no_dims) 地标的低维嵌入
      k2 : 地标层使用的近邻数（用于构造 P 的局部自适应核）
    """
    # 基本尺寸
    N, dim = X_samp.shape

    # 自适应确定 k2（邻域大小）
    #   - 小样本直接取 N 或固定值
    #   - 中等样本按比例（约 2%N + 常数）
    #   - 超大样本对数增长 + 常数，避免 k2 过大
 
    if N < 9:
        k2 = N
    else:
        if N > 1000:
            k2 = int(np.ceil(np.log2(N)) + 18)
        elif N > 50:
            k2 = int(np.ceil(0.02 * N)) + 8
        else:
            k2 = 9

    # 构造高维概率矩阵 P（仅在每行的 k2 个近邻上赋值 -> 稀疏）
    # 两种路径：
    #   1) k1>0：使用采样阶段的 SNN（共享近邻）思想修正距离（增强类内凝聚、抑制跨类吸引）
    #   2) k1=0：直接在 X_samp 上做 KNN，并用逐点带宽的高斯核
    if k1 > 0:
        # 用列表累积稀疏矩阵的行/列/值，最后一次性构造 csr_matrix
        row = []  # 行索引列表
        col = []  # 列索引列表
        Pval = [] # 非零值列表

        # (N, k1+1)：第 i 个地标的邻居（含自邻居）的 RNN 值，用于度量“共享邻居强度”
        knn_rnn_mat = rnn[get_knn[id_samp]]

        # 逐行构造：第 i 行仅在其前 k2 个“修正距离”最近的点上赋值
        for i in range(N):
            # snn_id[j, t] = 1 表示地标 j 的第 t 个邻居落在“地标 i 的邻居集合”内（有共享近邻）
            snn_id = np.isin(get_knn[id_samp], get_knn[id_samp[i]]).astype(int)  # (N, k1+1)
            # 与 i 存在至少一个共享邻居的地标行索引
            nn_id = np.where(np.max(snn_id, axis=1) == 1)[0]

            # snn：与 i 共享近邻的“强度”向量（强调枢纽邻居：RNN 大的邻居占更大权重）
            snn = np.zeros((1, N))
            snn[:, nn_id] = np.sum(knn_rnn_mat[nn_id] * snn_id[nn_id], axis=1)

            # 归一化共享强度 -> [0,1]；然后对原始欧氏距离乘以 (1 - snn)^agg_coef 做“软缩放”
            # 共享越强（类内关系越强），(1 - snn) 越小，修正后的距离越短 -> 更强的类内吸引
            mod_dis = (1 - snn / max(np.max(snn), np.finfo(float).tiny)) ** agg_coef \
                      * cdist(X_samp[i:i + 1, :], X_samp)         # (1, N)

            # 取该行前 k2 个最小修正距离的索引与数值
            sort_dis = np.sort(mod_dis, axis=1)                  # (1, N)
            idx = np.argsort(mod_dis, axis=1)                    # (1, N)
            mean_samp_dis_squared = np.square(np.mean(sort_dis[0, :k2]))  # 局部带宽（均值距离平方）

            # 高斯核：exp(-0.5 * d^2 / sigma^2)，仅对前 k2 个赋值
            Pval.extend(np.exp(
                -0.5 * np.square(sort_dis[0, :k2]) /
                np.maximum(mean_samp_dis_squared, np.finfo(float).tiny)
            ))
            # 写入对应的 (row, col)
            row.extend((i * np.ones((k2, 1))).flatten().tolist())
            col.extend(idx[0, :k2])

        # 组装成 (N, N) 稀疏矩阵 P（未对称/未归一化）
        P = csr_matrix((Pval, (row, col)), shape=(N, N))

    else:
        # 无采样信息：直接用 X_samp 做 KNN，再按逐点带宽的高斯核构造 P
        if N > 5000 and dim > 50:
            # 大规模高维：先 PCA 预降（保留 contri=0.8 方差），再做邻居搜索 -> 更快/更稳
            xx = init_pca(X_samp, no_dims, 0.8)
            samp_dis, samp_knn = NearestNeighbors(n_neighbors=k2).fit(xx).kneighbors(xx)
        else:
            samp_dis, samp_knn = NearestNeighbors(n_neighbors=k2).fit(X_samp).kneighbors(X_samp)

        # (N,): 每个点的局部带宽（其 k2 个邻居距离的均值平方）
        mean_samp_dis_squared = np.square(np.mean(samp_dis, axis=1))

        # (N, k2)：每行对其 k2 个邻居赋高斯权重（逐点带宽）
        Pval = np.exp(
            -0.5 * np.square(samp_dis) /
            np.maximum(mean_samp_dis_squared[:, np.newaxis], np.finfo(float).tiny)
        )

        # 直接用稀疏构造：行索引展开为 [0..N-1] 各重复 k2 次，列索引为 samp_knn.flatten()
        P = csr_matrix(
            (Pval.flatten(), ([i for i in range(N) for _ in range(k2)], samp_knn.flatten())),
            shape=(N, N)
        )

    # 对称化（P <- (P + P^T)/2），稳定相似度，兼顾 i->j 与 j->i
    # 仍保持稀疏格式
    P = (P + P.transpose()) / 2

    # 初始化低维嵌入 Y
    #   'le'  ：对称归一化拉普拉斯的最小特征向量（去掉平凡解） -> Laplacian Eigenmaps
    #   'pca' ：线性 PCA 投影
    #   'mds' ：经典 MDS
    if initialize == 'le':
        # 度矩阵（稀疏对角），注意 P.sum(axis=0) 返回 (1, N) 稀疏矩阵，先 flatten 成 1D
        Dg = diags(np.array(P.sum(axis=0)).flatten())
        # 对称归一化拉普拉斯： L = D^{1/2} (D - P) D^{1/2}
        L = np.sqrt(Dg) @ (Dg - P) @ np.sqrt(Dg)
        # 取最小的 no_dims+1 个特征对（SM=Smallest Magnitude），去掉第一个（常量向量）
        eigenvalues, eigenvectors = sp_linalg.eigs(L, k=no_dims + 1, which='SM')
        smallest_indices = np.argsort(np.abs(eigenvalues))
        Y = np.real(eigenvectors[:, smallest_indices[1:]])  # (N, no_dims)
        del Dg, L

    elif initialize == 'pca':
        Y = pca(X_samp, no_dims)

    elif initialize == 'mds':
        Y = mds(X_samp, no_dims)

    # 概率归一化：P 视作“联合概率矩阵”，对总和（减去 N 个对角自项）做归一化
    # 注意：此处 P 为 csr_matrix，np.sum(P) 返回标量
    P = P / (np.sum(P) - N)

    # Block 设定：把 N 行按块切分（每块 ~3000 行），分块计算梯度，降低内存峰值
    no_blocks = math.ceil(N / 3000)         # 需要的块数
    mark = np.zeros((no_blocks, 2))         # 每块的起止行号 [start, end]（闭区间）
    for i in range(no_blocks):
        start = i * math.ceil(N / no_blocks)
        end   = min((i + 1) * math.ceil(N / no_blocks) - 1, N - 1)
        mark[i, :] = [start, end]

    # 训练超参与动量变量
    #   - 学习率调度：warmup 后做余弦退火（max_alpha -> min_alpha）
    #   - preGrad：上一轮的梯度（动量）
    max_alpha = 2.5 * N  # 预热阶段较大的步长（按 N 放缩）
    min_alpha = 2 * N    # 退火最低步长
    warm_step = 10       # 预热轮数
    preGrad = np.zeros((N, no_dims))  # 动量缓存
    epoch = 1

    # 迭代优化（KLD 损失的近似梯度；log 内核：Q_ij = 1/(1 + log(1 + d^2)))
    # 与 learning_s 的区别：这里按块累计 Pgrad/Qgrad 和 sumQ
    while epoch <= T_epoch:
        # 学习率调度
        if epoch <= warm_step:
            alpha = max_alpha
        else:
            # 余弦退火：从 max_alpha 平滑衰减到 min_alpha
            alpha = min_alpha + 0.5 * (max_alpha - min_alpha) * (
                1 + np.cos(np.pi * ((epoch - warm_step) / (T_epoch - warm_step)))
            )

        # 分块累计梯度
        Pgrad = np.zeros((N, no_dims))  # 来源于 P（真实分布）的梯度部分
        Qgrad = np.zeros((N, no_dims))  # 来源于 Q（模型分布）的梯度部分
        sumQ = 0                        # 所有块的 Q1 总和（用于归一化 Q）

        for i in range(no_blocks):
            # 当前块的行索引（连续区间）
            idx = [j for j in range(int(mark[i, 0]), int(mark[i, 1]) + 1)]

            # 计算当前块与全体的低维平方距离 D
            D = cdist(Y[idx], Y) ** 2             # (len_blk, N)

            # 低维相似度核与其导数辅助项
            Q1  = 1 / (1 + np.log(1 + D))         # log-kernel，相比 t 分布更重尾，利于类内紧凑/收敛
            QQ1 = 1 / (1 + D)                     # 辅助项：对 (1 + log(1 + D)) 的链式导数中会出现
            del D

            # P 部分的梯度“权重矩阵”（注意这里对 P 是稀疏乘法，再 toarray 进入 dense 计算）
            # -4 * P[idx,:] ⊙ Q1 ⊙ QQ1
            # 负号是因为后续采用 (diag(row_sums) - Mat) @ Y 的拉普拉斯形式
            Pmat = -4 * P[idx, :].multiply(Q1).multiply(QQ1).toarray()

            # Q 部分的梯度“权重矩阵”：
            # -4 * (Q1^2) * QQ1   （Q 的归一化在块外通过 sumQ 统一处理）
            Qmat = -4 * Q1 ** 2 * QQ1
            del QQ1

            len_blk = len(idx)

            # 把每行的“对角位”减去行和：实现 (diag(row_sums) - Mat)
            # 这里 idPQ[:,1] = 块起始行 + [0..len_blk-1]，恰好对应全局行号的对角位置
            idPQ = np.column_stack((np.array(range(len_blk)), idx[0] + np.array(range(len_blk))))
            Pmat[idPQ[:, 0], idPQ[:, 1]] = Pmat[idPQ[:, 0], idPQ[:, 1]] - np.sum(Pmat, axis=1)
            Qmat[idPQ[:, 0], idPQ[:, 1]] = Qmat[idPQ[:, 0], idPQ[:, 1]] - np.sum(Qmat, axis=1)

            # 乘以 Y 得到梯度贡献： (diag(row_sums) - Mat) @ Y
            Pgrad[idx] = Pmat @ Y
            Qgrad[idx] = Qmat @ Y
            del Pmat, Qmat

            # 统计 Q 的归一化分母（全体 Q1 的总和，减去 N 的自项在块外统一处理）
            sumQ = sumQ + np.sum(Q1)

        # 组合总梯度并更新 Y：
        #   grad_total = Pgrad - Qgrad / (sumQ - N)
        #   动量项：((epoch-1)/(epoch+2)) * preGrad    （随轮数递增的动量系数）
        Y = Y - alpha * (Pgrad - Qgrad / (sumQ - N) + (epoch - 1) / (epoch + 2) * preGrad)
        preGrad = Pgrad - Qgrad / (sumQ - N)

        epoch = epoch + 1

    print(str(epoch - 1) + ' epochs have been computed!')
    return Y, k2